Exploring the mathematical universe – connections, contradictions, and kale

Science and maths skills are widely celebrated as keys to economic and technological progress, but abstract mathematics may seem bafflingly far from industrial optimisation or medical imaging. Pure mathematics often yields unanticipated applications, but without a time machine to look into the future, how do mathematicians like me choose what to study?

Over Thai noodles, I asked some colleagues what makes a problem interesting, and they offered a slew of suggestions: surprises, contradictions, patterns, exceptions, special cases, connections. These answers might sound quite different, but they all support a view of the mathematical universe as a structure to explore.

In this view, mathematicians are like anatomists learning how a body works, or navigators charting new waters. The questions we ask take many forms, but the most interesting ones are those that help us see the big picture more clearly.

Making maps

Mathematical objects come in many forms. Some of them are probably quite familiar, like numbers and shapes. Others might seem more exotic, like equations, functions and symmetries.

Instead of just naming objects, a mathematicians might ask how some class of objects is organised. Take prime numbers: we know there are infinitely many of them, but we need a structural understanding to work out how frequently they occur or to identify them in an efficient way.

Other good questions explore relationships between apparently different objects. For example, shapes have symmetry, but so do the solutions to some equations.

Classifying objects and finding connections between them help us assemble a coherent map of the mathematical world. Along the way, we sometimes encounter surprising examples that defy the patterns we’ve inferred.

Such apparent contradictions reveal where our understanding is still lacking, and resolving them provides valuable insight.

Consider the triangle

The humble triangle provides a famous example of an apparent contradiction. Most people think of a triangle as the shape formed by three connecting line segments, and this works well for the geometry we can draw on a sheet of paper.

However, this notion of triangle is limited. On a surface with no straight lines, like a sphere or a curly kale leaf, we need a more flexible definition.

So, to extend geometry to surfaces that aren’t flat, an open-minded mathematician might propose a new definition of a triangle: pick three points and connect each pair by the shortest path between them.

This is a great generalisation because it matches the familiar definition in the familiar setting, but it also opens up new terrain. When mathematicians first studied these generalised triangles in the 19th century, they solved a millennia-old mystery and revolutionised mathematics.

The parallel postulate problem

Around 300 BC, the Greek mathematician Euclid wrote a treatise on planar geometry called The Elements. This work presented both fundamental principles and results that were logically derived from them.

One of his principles, called the parallel postulate, is equivalent to the statement that the sum of the angles in any triangle is 180°. This is exactly what you’ll measure in every flat triangle, but later mathematicians debated whether the parallel postulate should be a foundational principle or just a consequence of the other fundamental assumptions.

This puzzle persisted until the 1800s, when mathematicians realised why a proof had remained so elusive: the parallel postulate is false on some surfaces.

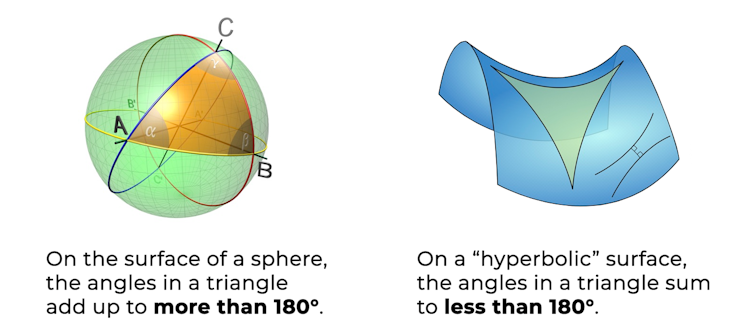
On a sphere, the sides of a triangle bend away from each other and the angles add up to more than 180°. On a rippled kale leaf, the sides bow in towards each other and the angle sum is less than 180°.

Triangles where the angle sum breaks the apparent rule led to the revelation that there are kinds of geometry Euclid never imagined. This is a deep truth, with applications in physics, computer graphics, fast algorithms, and beyond.

Salad days

People sometimes debate whether mathematics is discovered or invented, but both points of view feel real to those of us who study mathematics for a living. Triangles on a piece of kale are skinny whether or not we notice them, but selecting which questions to study is a creative enterprise.

Interesting questions arise from the friction between patterns we understand and the exceptions that challenge them. Progress comes when we reconcile apparent contradictions that pave the way to identify new ones.

Today we understand the geometry of two-dimensional surfaces well, so we’re equipped to test ourselves against similar questions about higher-dimensional objects.

In the past few decades we’ve learned that three-dimensional spaces also have their own innate geometries. The most interesting one is called hyperbolic geometry, and it turns out to act like a three-dimensional version of curly kale. We know this geometry exists, but it remains mysterious: in my own research field, there are lots of questions we can answer for any three-dimensional space … except the hyperbolic ones.

In higher dimensions we still have more questions than answers, but it’s safe to say that study of four-dimensional geometry is entering its salad days.